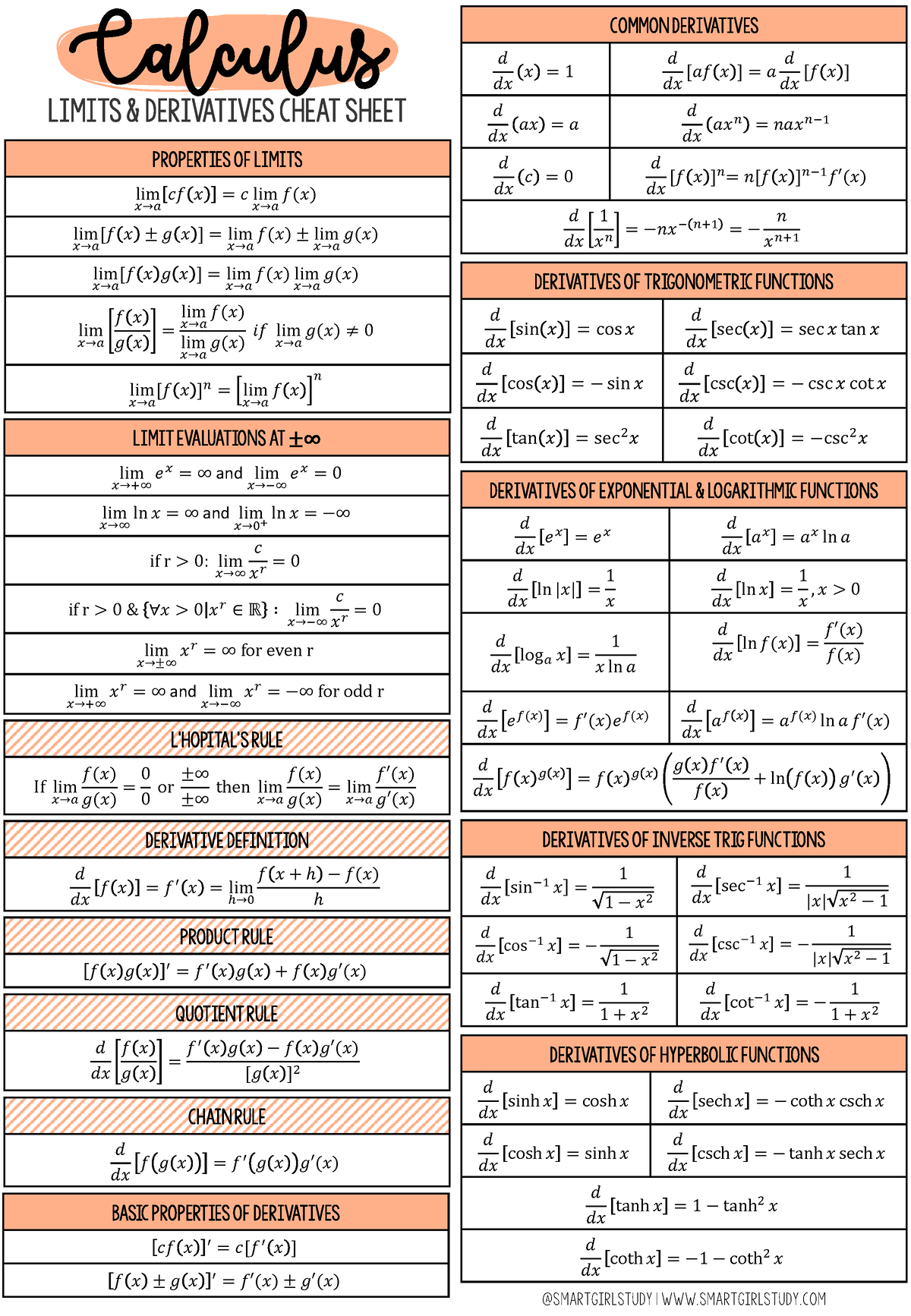
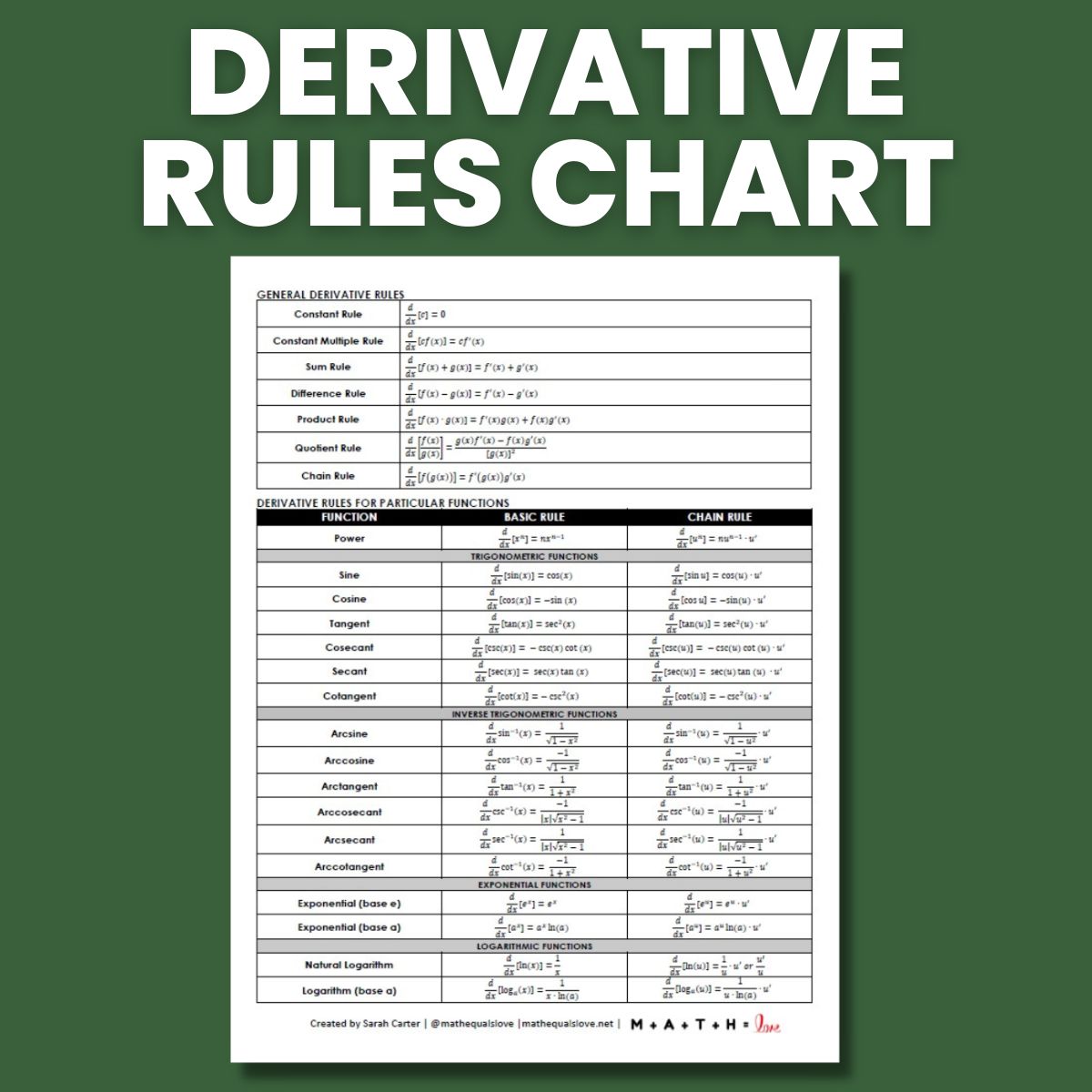
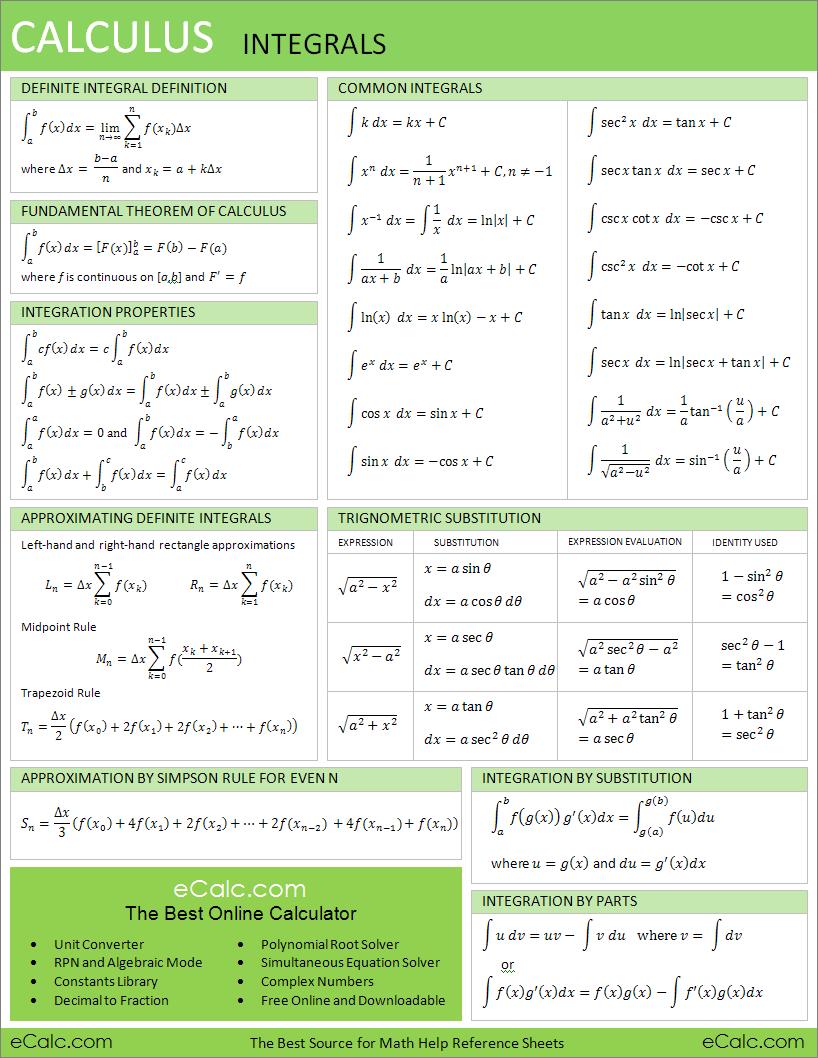
Calculus Derivatives Cheat Sheet
Calculus Derivatives Cheat Sheet - Add on a derivative every. Arc hyperbolic derivatives \frac{d}{dx}\left(\arcsinh(x))=\frac{1}{\sqrt{x^{2}+1}} \frac{d}{dx}\left(\arccosh(x))=\frac{1}{\sqrt{x. The chain rule applied to some specific functions. Write down equation relating quantities and differentiate with respect to t using implicit differentiation (i.e. ¢ f ¢¢ ( x ) = ( f ¢ ( x ) ).
Write down equation relating quantities and differentiate with respect to t using implicit differentiation (i.e. The chain rule applied to some specific functions. Add on a derivative every. ¢ f ¢¢ ( x ) = ( f ¢ ( x ) ). Arc hyperbolic derivatives \frac{d}{dx}\left(\arcsinh(x))=\frac{1}{\sqrt{x^{2}+1}} \frac{d}{dx}\left(\arccosh(x))=\frac{1}{\sqrt{x.
Add on a derivative every. ¢ f ¢¢ ( x ) = ( f ¢ ( x ) ). Arc hyperbolic derivatives \frac{d}{dx}\left(\arcsinh(x))=\frac{1}{\sqrt{x^{2}+1}} \frac{d}{dx}\left(\arccosh(x))=\frac{1}{\sqrt{x. Write down equation relating quantities and differentiate with respect to t using implicit differentiation (i.e. The chain rule applied to some specific functions.
Calculus Cheat Sheet Derivatives
Add on a derivative every. Arc hyperbolic derivatives \frac{d}{dx}\left(\arcsinh(x))=\frac{1}{\sqrt{x^{2}+1}} \frac{d}{dx}\left(\arccosh(x))=\frac{1}{\sqrt{x. The chain rule applied to some specific functions. Write down equation relating quantities and differentiate with respect to t using implicit differentiation (i.e. ¢ f ¢¢ ( x ) = ( f ¢ ( x ) ).
Calculus derivatives rules and limits cheat sheet eeweb Artofit
Arc hyperbolic derivatives \frac{d}{dx}\left(\arcsinh(x))=\frac{1}{\sqrt{x^{2}+1}} \frac{d}{dx}\left(\arccosh(x))=\frac{1}{\sqrt{x. ¢ f ¢¢ ( x ) = ( f ¢ ( x ) ). Add on a derivative every. Write down equation relating quantities and differentiate with respect to t using implicit differentiation (i.e. The chain rule applied to some specific functions.
Calculus Derivatives, Rules, and Limits Cheat Sheet EEWeb
The chain rule applied to some specific functions. Write down equation relating quantities and differentiate with respect to t using implicit differentiation (i.e. Arc hyperbolic derivatives \frac{d}{dx}\left(\arcsinh(x))=\frac{1}{\sqrt{x^{2}+1}} \frac{d}{dx}\left(\arccosh(x))=\frac{1}{\sqrt{x. ¢ f ¢¢ ( x ) = ( f ¢ ( x ) ). Add on a derivative every.
SOLUTION Calculus Derivatives Cheat Sheet Studypool
The chain rule applied to some specific functions. Arc hyperbolic derivatives \frac{d}{dx}\left(\arcsinh(x))=\frac{1}{\sqrt{x^{2}+1}} \frac{d}{dx}\left(\arccosh(x))=\frac{1}{\sqrt{x. ¢ f ¢¢ ( x ) = ( f ¢ ( x ) ). Add on a derivative every. Write down equation relating quantities and differentiate with respect to t using implicit differentiation (i.e.
Calculus Cheat Sheet i dont know la Limits & Derivatives Cheat
Write down equation relating quantities and differentiate with respect to t using implicit differentiation (i.e. ¢ f ¢¢ ( x ) = ( f ¢ ( x ) ). Add on a derivative every. The chain rule applied to some specific functions. Arc hyperbolic derivatives \frac{d}{dx}\left(\arcsinh(x))=\frac{1}{\sqrt{x^{2}+1}} \frac{d}{dx}\left(\arccosh(x))=\frac{1}{\sqrt{x.
Application of Derivatives (CALCULUS) formulas and concepts cheat sheet
Add on a derivative every. ¢ f ¢¢ ( x ) = ( f ¢ ( x ) ). Arc hyperbolic derivatives \frac{d}{dx}\left(\arcsinh(x))=\frac{1}{\sqrt{x^{2}+1}} \frac{d}{dx}\left(\arccosh(x))=\frac{1}{\sqrt{x. The chain rule applied to some specific functions. Write down equation relating quantities and differentiate with respect to t using implicit differentiation (i.e.
Calculus Cheat Sheet Derivatives Reduced1
Add on a derivative every. Write down equation relating quantities and differentiate with respect to t using implicit differentiation (i.e. The chain rule applied to some specific functions. Arc hyperbolic derivatives \frac{d}{dx}\left(\arcsinh(x))=\frac{1}{\sqrt{x^{2}+1}} \frac{d}{dx}\left(\arccosh(x))=\frac{1}{\sqrt{x. ¢ f ¢¢ ( x ) = ( f ¢ ( x ) ).
Derivative Rules Cheat Sheet
¢ f ¢¢ ( x ) = ( f ¢ ( x ) ). Arc hyperbolic derivatives \frac{d}{dx}\left(\arcsinh(x))=\frac{1}{\sqrt{x^{2}+1}} \frac{d}{dx}\left(\arccosh(x))=\frac{1}{\sqrt{x. The chain rule applied to some specific functions. Write down equation relating quantities and differentiate with respect to t using implicit differentiation (i.e. Add on a derivative every.
Derivatives of trig functions cheat sheet honbox
¢ f ¢¢ ( x ) = ( f ¢ ( x ) ). Add on a derivative every. Arc hyperbolic derivatives \frac{d}{dx}\left(\arcsinh(x))=\frac{1}{\sqrt{x^{2}+1}} \frac{d}{dx}\left(\arccosh(x))=\frac{1}{\sqrt{x. The chain rule applied to some specific functions. Write down equation relating quantities and differentiate with respect to t using implicit differentiation (i.e.
OCULUS REPAIRO Math notes, Studying math, Calculus notes
¢ f ¢¢ ( x ) = ( f ¢ ( x ) ). Add on a derivative every. Arc hyperbolic derivatives \frac{d}{dx}\left(\arcsinh(x))=\frac{1}{\sqrt{x^{2}+1}} \frac{d}{dx}\left(\arccosh(x))=\frac{1}{\sqrt{x. Write down equation relating quantities and differentiate with respect to t using implicit differentiation (i.e. The chain rule applied to some specific functions.
The Chain Rule Applied To Some Specific Functions.
Add on a derivative every. Arc hyperbolic derivatives \frac{d}{dx}\left(\arcsinh(x))=\frac{1}{\sqrt{x^{2}+1}} \frac{d}{dx}\left(\arccosh(x))=\frac{1}{\sqrt{x. ¢ f ¢¢ ( x ) = ( f ¢ ( x ) ). Write down equation relating quantities and differentiate with respect to t using implicit differentiation (i.e.