Trig Integrals Cheat Sheet

Trig Integrals Cheat Sheet - Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int f\left(x\right)dx\pm \int g\left(x\right)dx Currently this cheat sheet is 4 pages long. A unit circle (completely filled out) is also included. ( (𝑥))⋅ ′(𝑥) 𝑥=∫ ( ) , = (𝑥) definite integrals rules: (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→.

Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int f\left(x\right)dx\pm \int g\left(x\right)dx ( (𝑥))⋅ ′(𝑥) 𝑥=∫ ( ) , = (𝑥) definite integrals rules: (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→. Currently this cheat sheet is 4 pages long. A unit circle (completely filled out) is also included.

Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int f\left(x\right)dx\pm \int g\left(x\right)dx A unit circle (completely filled out) is also included. ( (𝑥))⋅ ′(𝑥) 𝑥=∫ ( ) , = (𝑥) definite integrals rules: (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→. Currently this cheat sheet is 4 pages long.

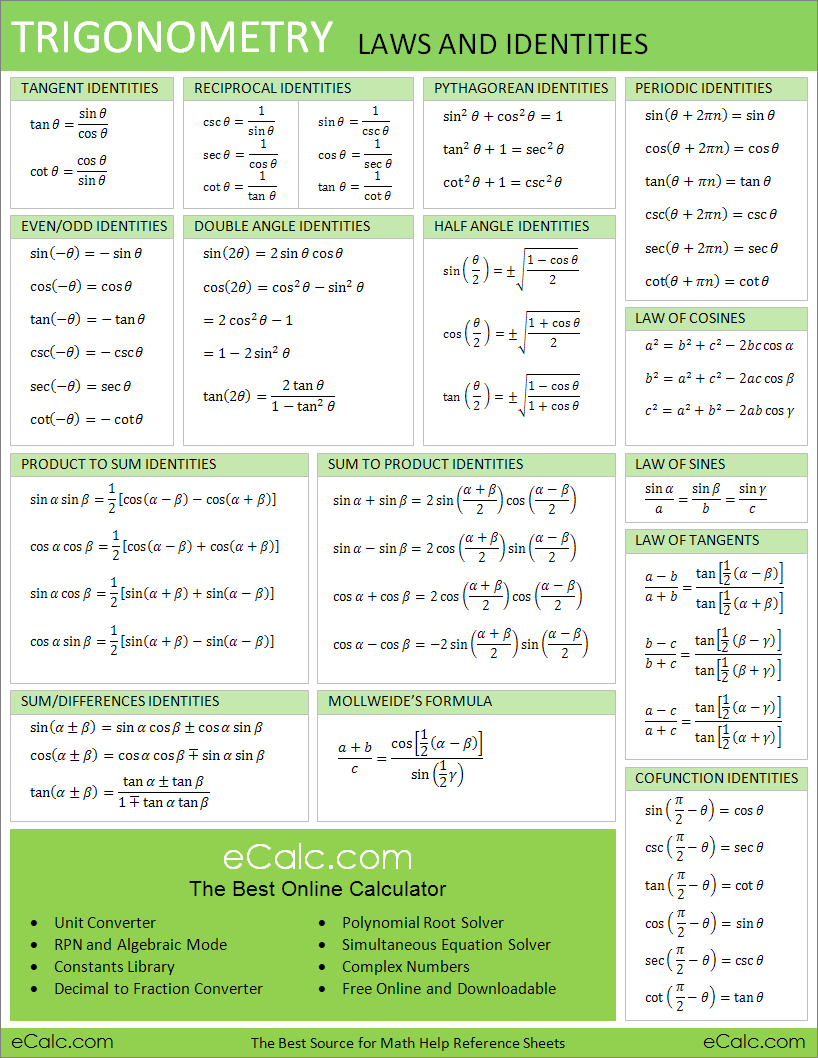
Complete table of integrals in a single sheet, Integrals of trig

( (𝑥))⋅ ′(𝑥) 𝑥=∫ ( ) , = (𝑥) definite integrals rules: (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→. A unit circle (completely filled out) is also included. Currently this cheat sheet is 4 pages long. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int f\left(x\right)dx\pm \int.

SOLUTION Trigonometric integrals cheat sheet Studypool

( (𝑥))⋅ ′(𝑥) 𝑥=∫ ( ) , = (𝑥) definite integrals rules: (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→. Currently this cheat sheet is 4 pages long. A unit circle (completely filled out) is also included. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int f\left(x\right)dx\pm \int.

Chapter 5 Trig Identities Mrs. Kramer, Laingsburg High School

A unit circle (completely filled out) is also included. Currently this cheat sheet is 4 pages long. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int f\left(x\right)dx\pm \int g\left(x\right)dx (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→. ( (𝑥))⋅ ′(𝑥) 𝑥=∫ ( ) , = (𝑥) definite integrals.

Trig Indefinite Integrals Cheat Sheet PDF

(𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→. ( (𝑥))⋅ ′(𝑥) 𝑥=∫ ( ) , = (𝑥) definite integrals rules: A unit circle (completely filled out) is also included. Currently this cheat sheet is 4 pages long. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int f\left(x\right)dx\pm \int.

Trig integrals cheat sheet nolfrite

(𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→. ( (𝑥))⋅ ′(𝑥) 𝑥=∫ ( ) , = (𝑥) definite integrals rules: Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int f\left(x\right)dx\pm \int g\left(x\right)dx Currently this cheat sheet is 4 pages long. A unit circle (completely filled out) is also.

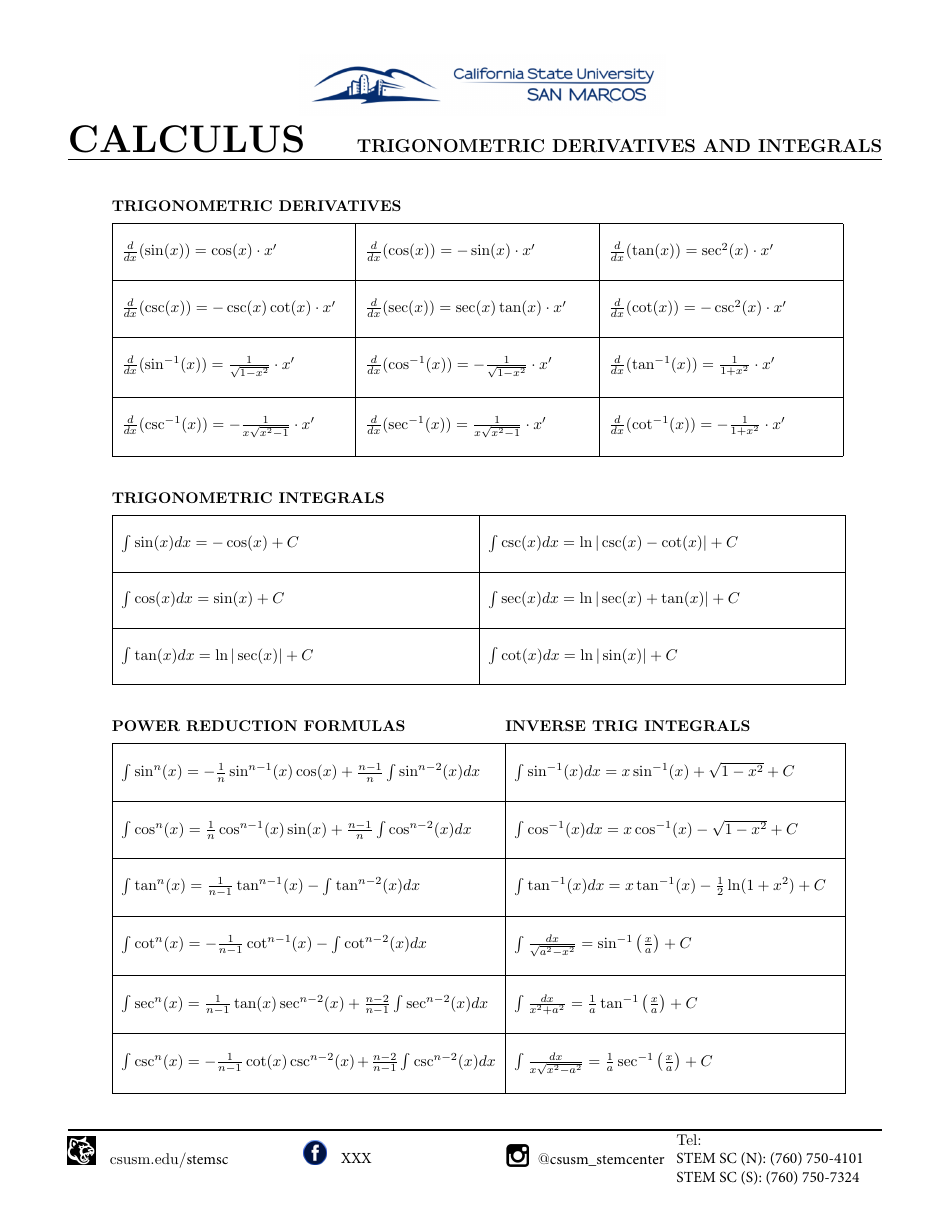
Derivatives and Integrals Cheat Sheet Download Printable PDF

(𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int f\left(x\right)dx\pm \int g\left(x\right)dx ( (𝑥))⋅ ′(𝑥) 𝑥=∫ ( ) , = (𝑥) definite integrals rules: Currently this cheat sheet is 4 pages long. A unit circle (completely filled out) is also.

Trig Integrals Table Pdf Review Home Decor

Currently this cheat sheet is 4 pages long. (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→. A unit circle (completely filled out) is also included. ( (𝑥))⋅ ′(𝑥) 𝑥=∫ ( ) , = (𝑥) definite integrals rules: Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int f\left(x\right)dx\pm \int.

Trigonometric Derivatives and Integrals Calculus Cheat Sheet Download

Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int f\left(x\right)dx\pm \int g\left(x\right)dx (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→. ( (𝑥))⋅ ′(𝑥) 𝑥=∫ ( ) , = (𝑥) definite integrals rules: A unit circle (completely filled out) is also included. Currently this cheat sheet is 4 pages.

SOLUTION algebra cheat sheet integral table, derivative table

(𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int f\left(x\right)dx\pm \int g\left(x\right)dx Currently this cheat sheet is 4 pages long. A unit circle (completely filled out) is also included. ( (𝑥))⋅ ′(𝑥) 𝑥=∫ ( ) , = (𝑥) definite integrals.

Calculus cheat sheet_integrals

(𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→. A unit circle (completely filled out) is also included. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int f\left(x\right)dx\pm \int g\left(x\right)dx ( (𝑥))⋅ ′(𝑥) 𝑥=∫ ( ) , = (𝑥) definite integrals rules: Currently this cheat sheet is 4 pages.

( (𝑥))⋅ ′(𝑥) 𝑥=∫ ( ) , = (𝑥) Definite Integrals Rules:

Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int f\left(x\right)dx\pm \int g\left(x\right)dx A unit circle (completely filled out) is also included. (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→. Currently this cheat sheet is 4 pages long.